Too Many Cooks Can Make Good Broth
Lately, I’ve been playing around with the poorly-named Structured Outputs, reading Three Easy Pieces, and cooking. (Un)naturally, I thought - how could I combine all three things?
Enter Recipe DAGger: a tiny tool to help a team of chefs attack a recipe in parallel.
How do we decide which chef does what, so that the recipe takes the least amount of time to complete?
One can think of a recipe as a directed acyclic graph (DAG) of tasks that need to be run (since steps in a recipe can either depend on previous steps or be independent).
So, I first used an LLM1 to go from recipe text to a DAG representation (i.e., structured output). I learnt that the Pydantic model (or schema) you want the LLM to return should not have default values or dict attributes. The latter is because a dict can have any value as a key, whereas a schema should have known keys. The takeaway: use an edge list to represent your DAG, and not an adjacency list.
Then, I applied the Coffman-Graham algorithm2 on this DAG to come up with a task sequence for each chef. Given the number of chefs n, this algorithm comes up with a list of at most n independent tasks for each time step – making a recipe parallelizable. One limitation of this algorithm is that it assumes each task takes unit time. Practically, this just means more break time for lucky chefs! Nah, I should probably address this. Soon.
Anyway, you can check out the progress here. I still need to make it pretty.
Update: 22 Feb, 2025
Recipe DAGger is now pretty!
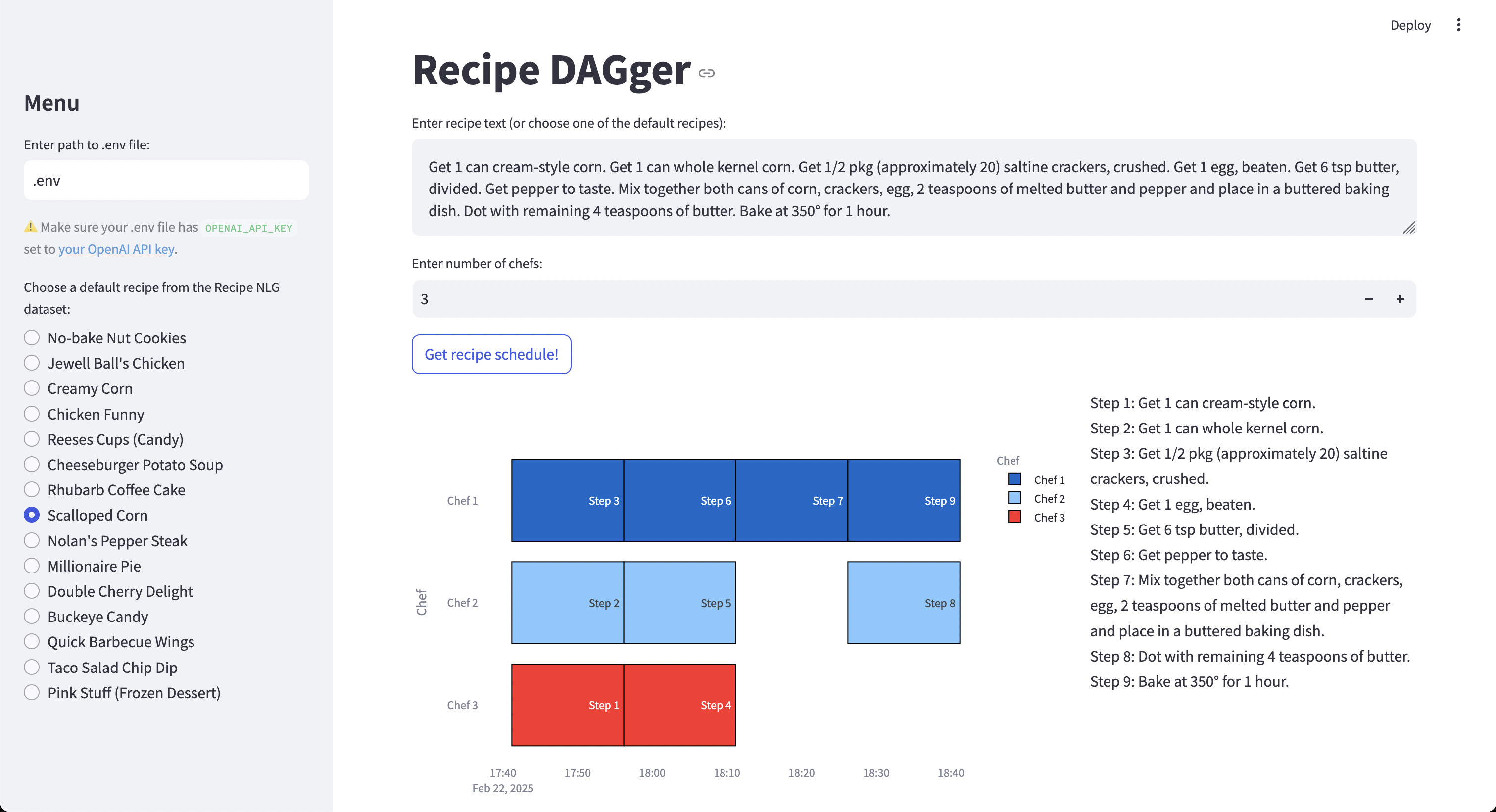
Recipe DAGger (Prettier Version). I used Streamlit for the overall UI, and Plotly to visualize the recipe schedule using a Gantt Chart.
There’s still some more work left to be done (parsing a recipe webpage to get well-formatted text), but hey, Recipe DAGger is on GitHub - contributions are welcome 😛.
-
This could have been overkill because the prompt I came up with could be converted into some simple Python code that does named entity recognition and builds the DAG. But buzzwords!!! ↩︎
-
Another cool application of this algorithm is graph drawing, a problem I just learnt about. ↩︎